Equação de Análise Empírica (Parte II)

Motivação

• Esta é uma primeira aproximação para o problema de análise multivariado
• Isto significa que, na prática, estamos tratando de um conjunto (ou uma série) de observações de quantidades diferentes (e.g., temperatura, vento e pressão)
• Quanto maior a quantidade de variáveis, mais complexo torna-se a determinação da análise

Equação de Análise Empírica (Parte II)

Motivação

• No problema multivariado, procuramos uma solução ("análise") que represente o melhor ajustamento do background às observações
• No exemplo mais simples da equação de análise empírica, tínhamos apenas uma equação de análise para uma única variável
• Para que possamos extrapolar o problema para variáveis, será necessário calcular análises, uma para cada variável de estado:

• Onde:
  • : é o vetor análise da enésima variável
  • : é o vetor background da enésima variável
  • : é o vetor observação da enésima variável
  • : é um vetor com os pesos dado à observação
  • : é um vetor com os pesos dado ao background)

Equação de Análise Empírica (Parte II)

Motivação

• O problema de análise meteorológica multivariada considera uma modelo real
• Aqui iremos considerar três vetores de quantidades diferentes (), com 100 elementos cada:

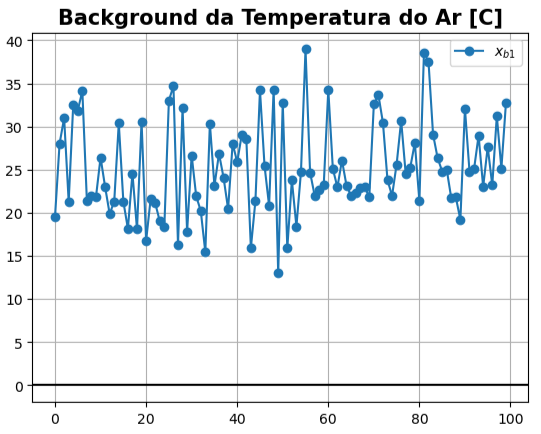
# Background da Temperatura do Ar [C]

xb1 = 40. + (15. - 40.) * np.random.randn(100)

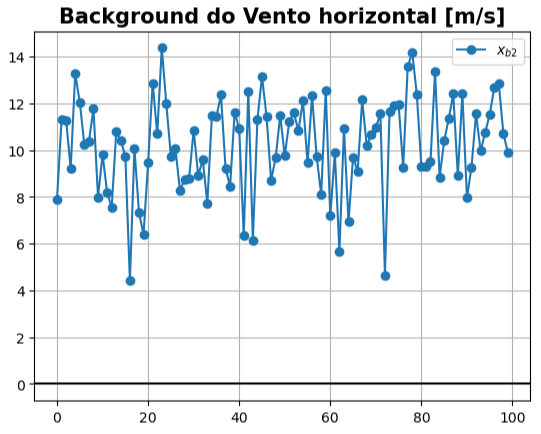
# Background do Vento horizontal [m/s]

xb2 = 10. + (5. - 10.) * np.random.randn(100)

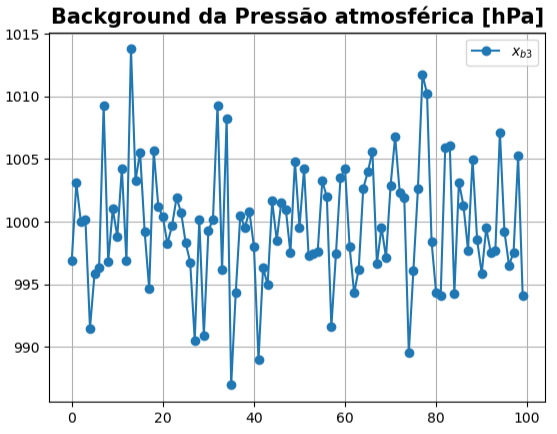
# Background da Pressão atmosférica [hPa]

xb3 = 1000. + (900. - 1000.) * np.random.randn(100)

Equação de Análise Empírica (Parte II)

Como é ?

xb1 = 
array([19.54359935, 28.02021832, 30.98934044, 21.29726065, 32.56254133,
       31.8798683 , 34.13027803, 21.33664531, 21.96966767, 21.87727694,
       26.41032294, 22.99802959, 19.86384305, 21.32748374, 30.38724682,
       21.3261903 , 18.16201694, 24.57677935, 18.0893644 , 30.58842399,
       16.75320872, 21.63775359, 21.11443669, 19.0322476 , 18.37576997,
       33.01617276, 34.70433601, 16.31712342, 32.13082557, 17.82616606,
       26.66327265, 21.91639599, 20.23068034, 15.43864126, 30.34930418,
       23.11258195, 26.86457668, 24.09901207, 20.45145304, 28.0368117 ,
       25.87652879, 29.05946519, 28.61622933, 15.91877439, 21.39591895,
       34.21444117, 25.44670878, 20.83541226, 34.27741552, 12.99872417,
       32.75729193, 15.91613634, 23.78639266, 18.42468865, 24.74387703,
       38.95803083, 24.68469212, 22.02186921, 22.65711468, 23.23432154,
       34.25743876, 25.09714219, 22.96486527, 26.08260443, 23.15910244,
       21.98108886, 22.31604543, 22.92486911, 22.99488973, 21.81249145,
       32.57957489, 33.68072417, 30.42811791, 23.79145663, 21.97971722,
       25.6181129 , 30.68512111, 24.47503308, 25.25955577, 28.11589535,
       21.35453516, 38.56106636, 37.53606813, 29.09164144, 26.36495428,
       24.80991689, 25.01314896, 21.70033864, 21.80864972, 19.19196652,
       32.08225608, 24.80684239, 25.06585103, 28.95608575, 23.01383423,
       27.62959653, 23.19876776, 31.23178029, 25.12522783, 32.70664654])

Equação de Análise Empírica (Parte II)

Como é ?

xb2 = 
array([ 7.89139469, 11.31710662, 11.25834407,  9.22292483, 13.26257547,
       12.04543631, 10.23465704, 10.36606995, 11.76295757,  7.99277442,
        9.80580539,  8.19489576,  7.54437886, 10.77591642, 10.39955475,
        9.74753976,  4.40891481, 10.06259102,  7.3239466 ,  6.40381252,
        9.46414692, 12.86896694, 10.69276845, 14.36733922, 11.97592713,
        9.73146508, 10.05474521,  8.27184444,  8.75321919,  8.80315983,
       10.85022741,  8.91140828,  9.58006867,  7.72998353, 11.46220732,
       11.43792601, 12.36487809,  9.21566116,  8.44912914, 11.61916852,
       10.90650476,  6.34443491, 12.49797447,  6.137198  , 11.31107992,
       13.1470192 , 11.44730413,  8.71090181,  9.67011543, 11.48149101,
        9.75057685, 11.23484438, 11.59826051, 10.82835328, 12.11049565,
        9.45548633, 12.33087288,  9.73940959,  8.09861212, 12.55259241,
        7.18805016,  9.87995869,  5.67240723, 10.94419448,  6.92951379,
        9.70143301,  9.08007802, 12.14802447, 10.19793865, 10.65233924,
       10.963924  , 11.55152817,  4.6441757 , 11.63745689, 11.90119717,
       11.95825119,  9.24286262, 13.58813583, 14.1642769 , 12.37186956,
        9.28553247,  9.31752349,  9.51763214, 13.34954962,  8.8345092 ,
       10.39238047, 11.3412283 , 12.399684  ,  8.90520432, 12.40032624,
        7.96678845,  9.26881557, 11.5502632 ,  9.96591038, 10.74955336,
       11.52074654, 12.65951626, 12.83326151, 10.69785151,  9.89670125])

Equação de Análise Empírica (Parte II)

Como é ?

xb3 = 
array([ 996.8880361 , 1003.08115118,  999.97617233, 1000.13327105,
        991.48361216,  995.84976209,  996.30653723, 1009.25491845,
        996.80281331, 1000.99401558,  998.82142829, 1004.24289653,
        996.85664595, 1013.77033688, 1003.30592647, 1005.52232586,
        999.20686366,  994.62184684, 1005.62742472, 1001.21459687,
       1000.35459829,  998.23323007,  999.64235681, 1001.87986157,
       1000.74507721,  998.31270317,  996.75214155,  990.52501866,
       1000.13389647,  990.90515357,  999.29005444, 1000.16553518,
...
       1002.3361858 , 1001.92798636,  989.55063344,  996.0905916 ,
       1002.60934246, 1011.72141294, 1010.22879591,  998.3758843 ,
        994.29775049,  994.11825428, 1005.92686155, 1006.06681313,
        994.25509972, 1003.12838654, 1001.28261554,  997.71676649,
       1004.9775312 ,  998.53027327,  995.86847976,  999.47741406,
        997.51047478,  997.69112758, 1007.13809055,  999.19446492,
        996.51733075,  997.52204916, 1005.22600936,  994.10177179])

Equação de Análise Empírica (Parte II)

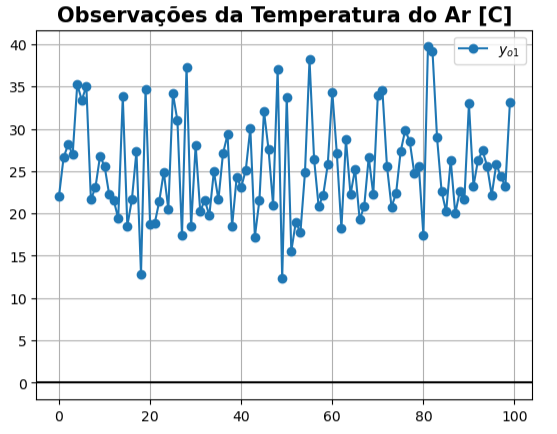
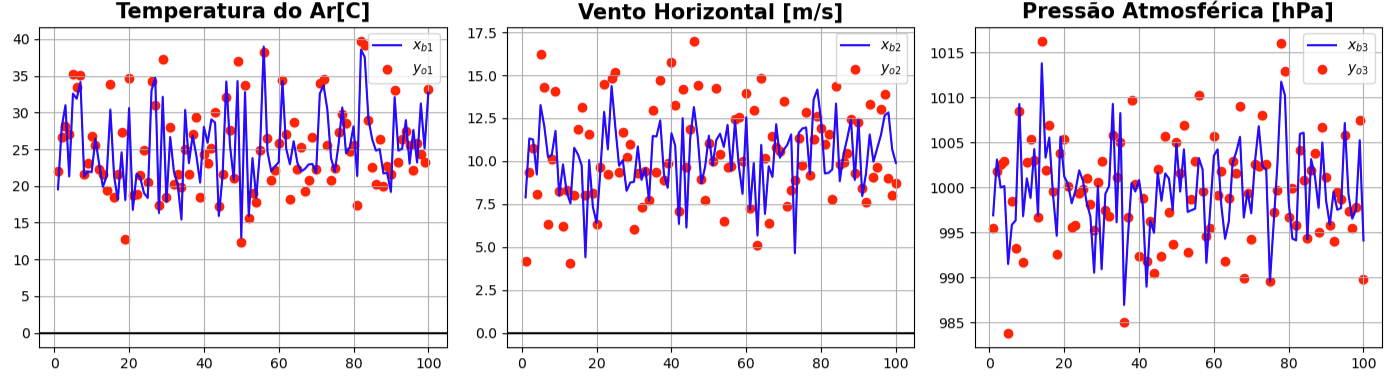
As observações

• O vetor observação para cada variável, pode ser definido de forma semelhante ao vetor background (), também com 100 elementos cada:

# Observações da Temperatura do Ar [C]

yo1 = xb1 + np.random.randn(100) * 3

# Observações do Vento Horizontal [m/s]

yo2 = xb2 + np.random.randn(100) * 2

# Observações da Pressão Atmosférica [hPa]

yo3 = xb3 + np.random.randn(100) * 4

Equação de Análise Empírica (Parte II)

Como é ?

yo1 = 
array([22.0712393 , 26.58791013, 28.14805192, 26.98159477, 35.23399823,
       33.40008597, 35.02158103, 21.64167556, 23.09235864, 26.7581439 ,
       25.60250411, 22.2851952 , 21.60054999, 19.41337962, 33.7859359 ,
       18.53437012, 21.64275727, 27.34204402, 12.81279131, 34.61906076,
       18.6932917 , 18.81008501, 21.40062741, 24.91801653, 20.4940796 ,
       34.1893406 , 30.95190393, 17.3819934 , 37.31104736, 18.46502053,
       28.05084568, 20.2676145 , 21.5593682 , 19.7744258 , 24.96566195,
       21.62261741, 27.08820325, 29.31410656, 18.47973529, 24.25416472,
       23.12769184, 25.10136771, 30.06111044, 17.24273538, 21.58330026,
       32.09020677, 27.56474563, 20.99475289, 37.04195311, 12.30406384,
       33.76675972, 15.56992676, 19.0061655 , 17.73779978, 24.84337806,
       38.15450086, 26.43742924, 20.82705709, 22.167535  , 25.75664848,
       34.35961501, 27.05852421, 18.23826217, 28.72354137, 22.2294522 ,
       25.26755696, 19.3101514 , 20.79101783, 26.64385568, 22.23610238,
       33.97735421, 34.55946135, 25.60156092, 20.78207244, 22.35560579,
       27.30155886, 29.82928653, 28.50606377, 24.75882271, 25.58798664,
       17.42761893, 39.6890225 , 39.15795835, 28.94022484, 22.60972549,
       20.20794155, 26.31603038, 19.99710402, 22.62536126, 21.65909853,
       32.96625744, 23.24176136, 26.33734637, 27.40711608, 25.58098425,
       22.14474225, 25.83748607, 24.34837869, 23.21031925, 33.13453801])

Equação de Análise Empírica (Parte II)

Como é ?

yo2 = 
array([ 4.18988815,  9.37460392, 10.7679655 ,  8.08458289, 16.24926569,
       14.30108474,  6.34047062, 10.11426126, 14.09465821,  8.26598524,
        6.19730716,  8.29706497,  4.0623404 ,  8.03324816, 11.85340907,
       13.14495454,  8.00195819, 11.57660517,  8.1154758 ,  6.32452072,
        9.64820965, 14.46329132,  9.24828971, 14.83472054, 15.1515784 ,
        9.33063813, 11.66734283, 10.20817894, 10.98699244,  6.04775072,
        9.31817934,  7.31846018,  9.42840878,  7.70830378, 12.93872419,
        9.33040986, 14.71326609,  8.86910384,  9.87305228, 15.76476408,
       13.24045813,  7.08111694, 14.1661612 ,  9.66428437, 11.87480323,
       16.97683911, 14.41572863,  8.94345535,  7.70911464, 11.02959723,
        9.99683187, 14.25997444, 10.43025165,  6.48407951,  9.6280322 ,
        9.71360869, 12.4138513 , 12.55751427,  9.99558739, 13.94852094,
        7.24681151, 12.98547236,  5.09213004, 14.8447996 , 10.14896282,
        6.4149297 , 11.43117218, 10.8370425 , 10.57713658, 13.51488394,
        7.37022493,  8.27861087,  8.87446208, 11.36219167,  9.73951402,
       12.8774461 ,  9.18332148, 11.28477962, 12.60024827, 11.91527289,
       10.96071101, 11.54910071,  7.75694468, 14.38380282,  9.82274468,
        9.92127001, 10.45692836, 12.44088767,  9.28426727, 12.27024771,
        8.43691615,  7.58471303, 13.33268913,  9.08476341,  9.67142117,
       13.02589387, 13.91438012,  9.00037576,  8.02441626,  8.72835341])

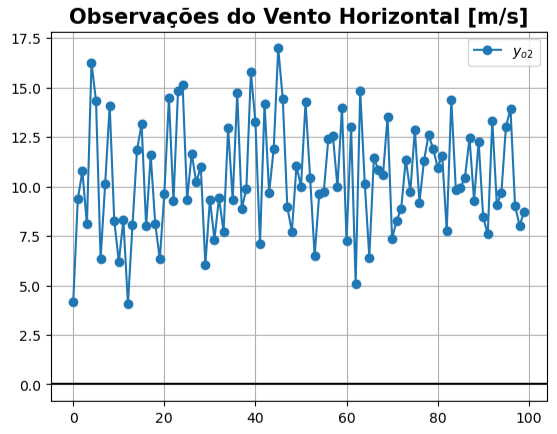
Equação de Análise Empírica (Parte II)

Como é ?

yo3 = 
array([ 995.46316584, 1001.83815365, 1002.60629618, 1002.882721  ,
        983.82955436,  998.42540759,  993.19980189, 1008.50573968,
        991.63923891, 1002.76353549, 1005.29946407, 1003.01109624,
        996.67824433, 1016.21970947, 1001.89346797, 1006.87587711,
        999.56306358,  992.52894043, 1003.81577561, 1005.3324725 ,
       1000.09066672,  995.57530359,  995.84004824,  999.35118141,
        999.74341359, 1000.98364998,  998.16868078,  995.22958019,
       1000.61306458, 1002.91621345,  997.41256208,  996.78433782,
       1005.76732347, 1001.16371745, 1004.98966941,  984.96552927,
        996.72893495, 1009.66660445, 1000.3310859 ,  992.31033854,
...
       1002.8943125 , 1001.618645  , 1009.0051308 ,  989.95562809,
        999.31630638,  994.19262375, 1002.59573404, 1002.29933836,
       1007.97648708, 1002.54962032,  989.61380801,  997.25814489,
        999.72884701, 1016.03008064, 1012.93582964,  996.65227536,
        999.88912342,  995.78890099, 1004.14727779, 1000.75434206,
        994.37429118, 1001.94229288, 1003.77489436,  995.0048657 ,
       1006.63879362, 1001.15311692,  995.76838989,  994.02725587,
        999.48654633,  998.64811864, 1005.76593828,  997.35828967,
        995.42593429,  997.83286157, 1007.4028775 ,  989.8213993 ])

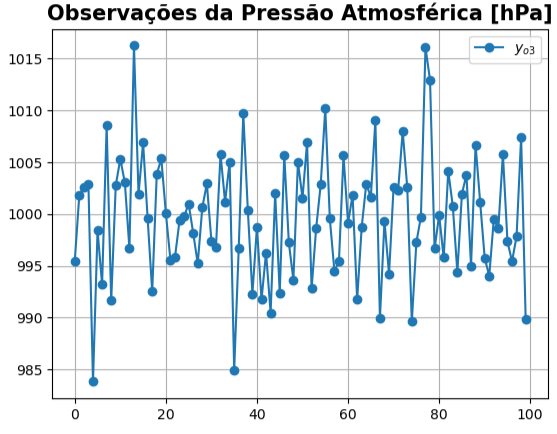
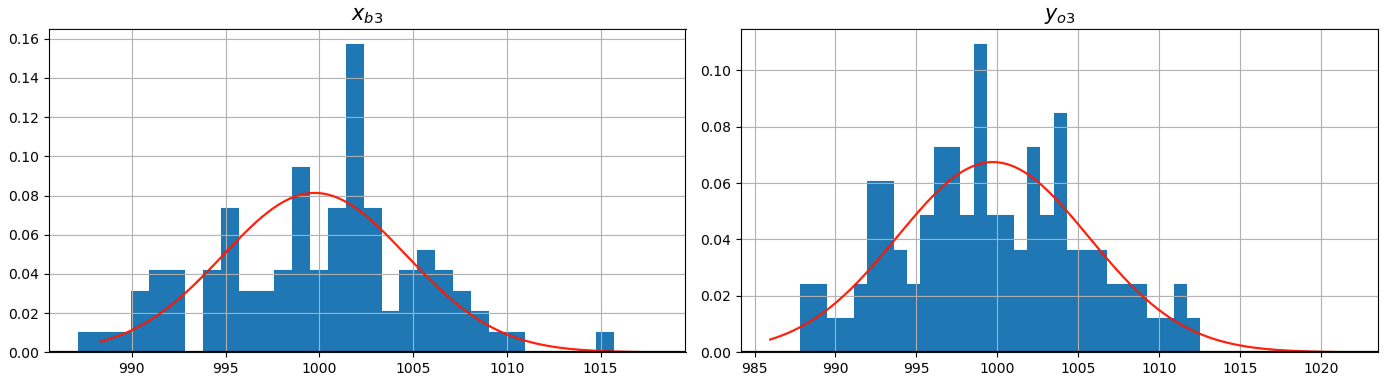
Equação de Análise Empírica (Parte II)

Distribuição Normal

• Observe que e possuem distribuições próximas da normal:

Equação de Análise Empírica (Parte II)

Distribuição Normal

• Observe que e possuem distribuições próximas da normal:

Equação de Análise Empírica (Parte II)

Distribuição Normal

• Observe que e possuem distribuições próximas da normal:

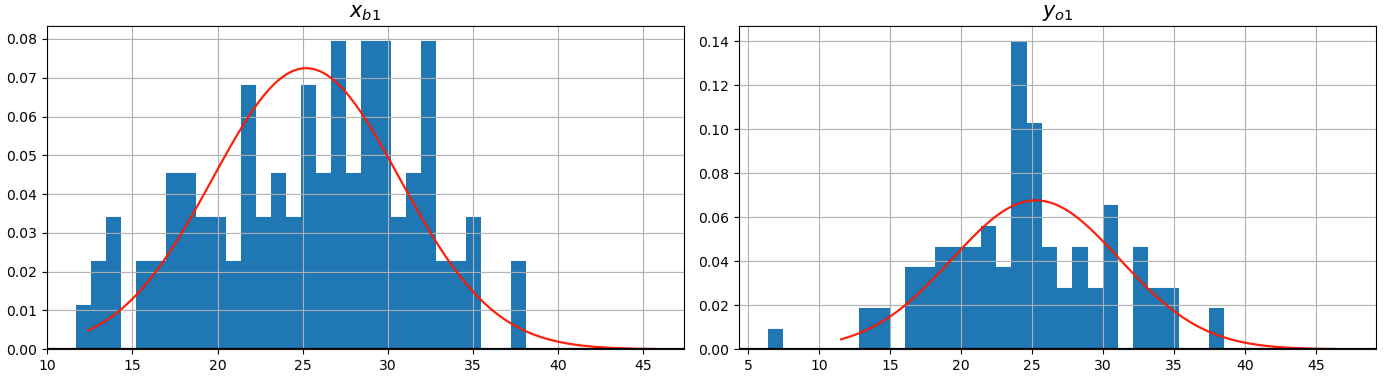
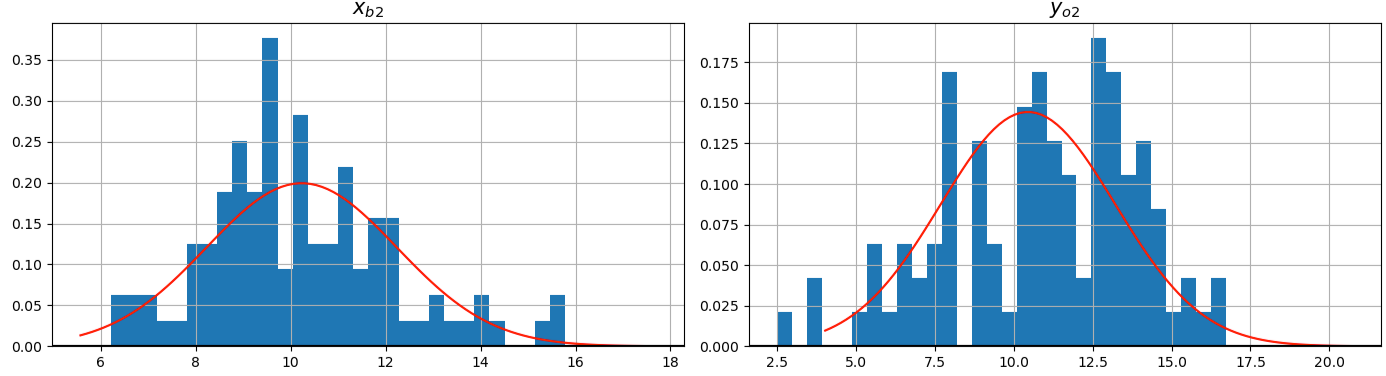
Equação de Análise Empírica (Parte II)

Séries de e

• Com e definidos, podemos plotar os seus elementos:

Equação de Análise Empírica (Parte II)

Determinação de (continua...)

• Antes de determinarmos o parâmetro , precisamos saber o que ele é e como pode ser definido
• é um parâmetro que relaciona as medidas das variâncias do background e das observações:

• Onde:
  • : é o enésimo vetor com as variâncias do background
  • : é o enésimo vetor com as variâncias das observações

• Os valores destes vetores são obtidos a partir das matrizes de covariâncias dos erros de background e observação
• Então, para calcular , precisamos determinar as matrizes de covariâncias dos erros de e , as quais denominaremos e , respectivamente

Equação de Análise Empírica (Parte II)

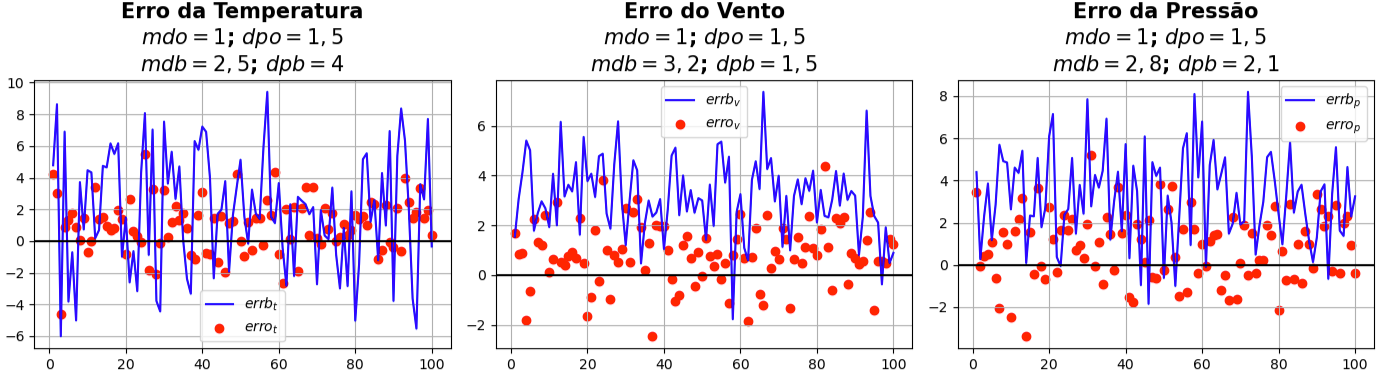
Erros e

• Vamos considerar que os erros dos elementos dos vetores e são randômicos, ou seja:
  • Não há relação entre os elementos dos dois vetores e
  • Os erros dos elementos dos vetores e são randômicos, ou seja, não há relação entre os erros dos elementos do vetor background e entre os elementos do vetor observação
• Manteremos a distribuição destes erros de forma conhecida, vamos manter uma distribuição próxima à normal de forma que possamos controlar a média e o desvio padrão

Equação de Análise Empírica (Parte II)

Erros e

# Erro da Temperatura do ar [C]

errot = mdot + dpot * np.random.randn(len(x0)) # mdot = 1;   dpot = 1.5
errbt = mdbt + dpbt * np.random.randn(len(x0)) # mdbt = 2.5; dpbt = 4

# Erro do Vento horizontal [m/s]

errov = mdov + dpov * np.random.randn(len(x0)) # mdov = 1;   dpov = 1.5
errbv = mdbv + dpbv * np.random.randn(len(x0)) # mdbv = 3.2; dpbv = 1.5

# Erro da Pressão atmosférica [hPa]

errop = mdop + dpop * np.random.randn(len(x0)) # mdop = 1;   dpop = 1.5
errbp = mdbp + dpbp * np.random.randn(len(x0)) # mdbp = 2.8; dpbp = 2.1

Equação de Análise Empírica (Parte II)

Determinação de (continuação)

Equação de Análise Empírica (Parte II)

Determinação de

Matrizes de covariâncias e

• Utilizaremos os vetores e para montar a matriz de erros de e :

xberr = [errbt, errbv, errbp]
yerr = [errot, errov, errop]

• O objetivo é calcular os pesos ( e ) para cada uma das variáveis
• depende das variâncias dos erros de observação e background
• Portanto, precisamos calcular as variâncias de e

Equação de Análise Empírica (Parte II)

Determinação de

Matrizes de covariâncias e

B = np.cov(xberr)
B =
array([[13.60650668, -0.31684168, -0.51769936],
       [-0.31684168,  2.28237194, -0.28122762],
       [-0.51769936, -0.28122762,  4.61157545]])

R = np.cov(yerr)
R = 
array([[ 2.75319186,  0.32594188,  0.16132722],
       [ 0.32594188,  1.54012175, -0.04601199],
       [ 0.16132722, -0.04601199,  2.59092547]])

xbvar = np.diag(B)
xbvar = array([13.60650668,  2.28237194,  4.61157545])

yvar = np.diag(R)
yvar = array([2.75319186, 1.54012175, 2.59092547])

Equação de Análise Empírica (Parte II)

Determinação de

• Cálculo de para cada uma das variáveis (temperatura, vento e pressão):

alphat = xbvar[0] / (xbvar[0] + yvar[0])
alphat = 0.8317088881282084

alphav = xbvar[1] / (xbvar[1] + yvar[1])
alphav = 0.5970897856560147

alphap = xbvar[2] / (xbvar[2] + yvar[2])
alphap = 0.6402741905463747

Equação de Análise Empírica (Parte II)

Cálculo de

• Observando novamente a equação da análise, notamos que todos os parâmetros estão determinados:

• Onde:
  • : é o vetor análise da enésima variável
  • : é o vetor background da enésima variável
  • : é o vetor observação da enésima variável
  • : é um vetor com os pesos dado à observação
  • : é um vetor com os pesos dado ao background)

Equação de Análise Empírica (Parte II)

Cálculo de

xat = alphat * yo1 + (1 - alphat) * xb1

xat = 
array([21.64585996, 26.82895487, 28.62621553, 26.02497186, 34.78441578,
       33.14424685, 34.87158266, 21.59034168, 22.90341972, 25.93673737,
       25.73845284, 22.40515889, 21.30827765, 19.73550633, 33.21396673,
       19.00420864, 21.05697961, 26.87667455, 13.70079166, 33.94074042,
       18.36679298, 19.2859565 , 21.35246406, 23.92749393, 20.13758692,
       33.99190688, 31.5834049 , 17.20278525, 36.43926208, 18.35750701,
       27.81732948, 20.54508977, 21.33576184, 19.0447518 , 25.87168108,
       21.8733652 , 27.05056888, 28.43645251, 18.81155787, 24.89075059,
       23.59029667, 25.76748034, 29.81794979, 17.01992451, 21.55176565,
       32.44769654, 27.20829886, 20.96793727, 36.576706  , 12.420969  ,
       33.59687526, 15.62819075, 19.81063524, 17.85339707, 24.82663292,
       38.28972781, 26.14245916, 21.02813335, 22.24992691, 25.33216327,
       34.34241965, 26.72844105, 19.03370746, 28.27909516, 22.38590408,
       24.71447359, 19.81601665, 21.15012603, 26.02976714, 22.16481243,
       33.74212037, 34.4115777 , 26.41382757, 21.28852505, 22.29234708,
       27.01824987, 29.97331588, 27.82767713, 24.84309164, 26.01341121,
       18.08848403, 39.49919751, 38.88500865, 28.96570691, 23.24169712,
       20.9824131 , 26.09676702, 20.28374327, 22.48791597, 21.24390214,
       32.81748786, 23.50515058, 26.123365  , 27.66779391, 25.14895572,
       23.06779448, 25.39341323, 25.506794  , 23.53258134, 33.06252768])

Equação de Análise Empírica (Parte II)

Cálculo de

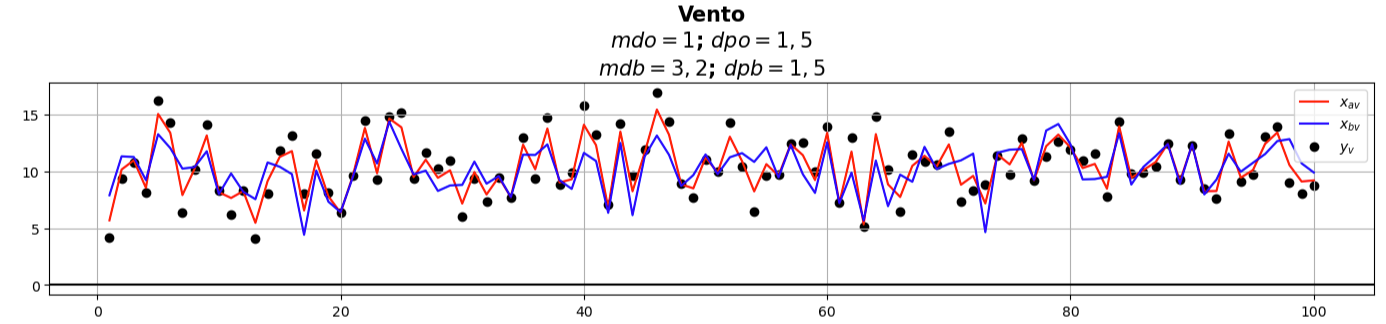
xav = alphav * yo2 + (1 - alphav) * xb2

xav = 
array([ 5.68126295, 10.1572581 , 10.96554403,  8.54323248, 15.04589769,
       13.39226095,  7.90947811, 10.21571755, 13.1551922 ,  8.15590581,
        7.65120796,  8.25589995,  5.46528926,  9.13829722, 11.26763631,
       11.77610142,  6.55428431, 10.9665934 ,  7.7965606 ,  6.35646819,
        9.57404889, 13.82092174,  9.83028495, 14.64640784, 13.87207607,
        9.4921354 , 11.01761077,  9.42800999, 10.08698238,  7.15793319,
        9.93545716,  7.96027524,  9.4895141 ,  7.71703878, 12.34382046,
       10.17954964, 13.76707657,  9.00873533,  9.2993391 , 14.09446129,
       12.30008448,  6.78430023, 13.49403173,  8.24318524, 11.64767335,
       15.43376555, 13.21972008,  8.84975715,  8.49922189, 11.21166985,
        9.89761321, 13.04111864, 10.90085435,  8.23443179, 10.62824208,
        9.60960856, 12.38041845, 11.42207111,  9.23127668, 13.38608708,
        7.22313596, 11.73422918,  5.32592965, 13.27320596,  8.85181392,
        7.73909545, 10.48389233, 11.36525053, 10.42435386, 12.36153544,
        8.81816299,  9.59730268,  7.17003649, 11.47309884, 10.61047824,
       12.50709308,  9.20731121, 12.21282537, 13.23041138, 12.09924035,
       10.28576446, 10.64997545,  8.46634364, 13.96709164,  9.42457451,
       10.11108523, 10.81322184, 12.42428629,  9.13153894, 12.32265768,
        8.2474969 ,  8.26325515, 12.61453152,  9.43978652, 10.10581164,
       12.41945464, 13.40878265, 10.54468458,  9.10157063,  9.19909269])

Equação de Análise Empírica (Parte II)

Cálculo de

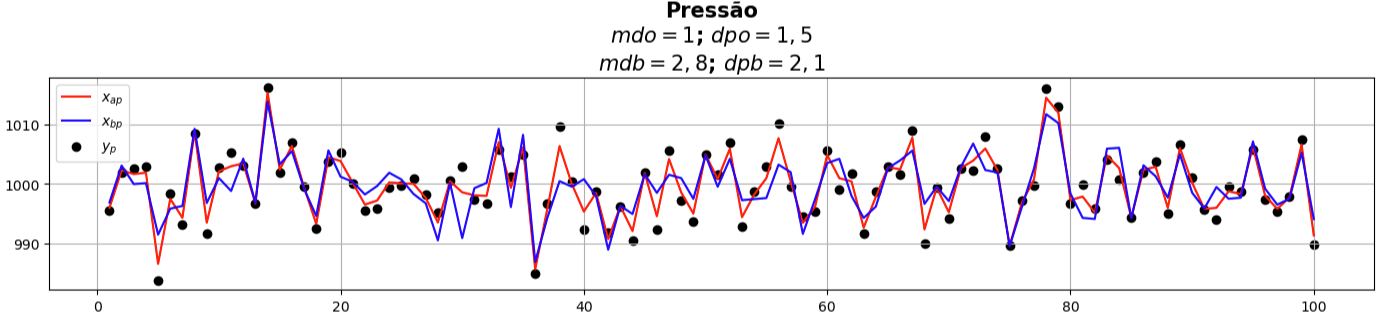
xap = alphap * yo3 + (1 - alphap) * xb3

xap = 
array([ 995.97572845, 1002.28529195, 1001.66017275, 1001.89367289,
        986.5829165 ,  997.49888143,  994.31737477, 1008.77523862,
        993.49670989, 1002.12699351, 1002.96914741, 1003.45420659,
        996.74242   , 1015.33860694, 1002.40156575, 1006.38896979,
        999.43492928,  993.28181289, 1004.46747255, 1003.85116636,
       1000.18560972,  996.53142834,  997.20783677, 1000.26081293,
       1000.10373785, 1000.02284147,  997.65911506,  993.53722799,
       1000.44069544,  998.59552522,  998.08794454,  998.00064178,
       1007.02729788,  999.3498906 , 1006.16150425,  985.67556906,
...
       1000.96499715, 1000.43367156,  992.66057211,  997.83467532,
       1002.80930211, 1002.4613988 , 1007.78060607,  992.36485176,
        999.39430704,  995.24780232, 1002.70102879, 1003.91223628,
       1005.94752513, 1002.32600254,  989.59108249,  996.83814584,
       1000.76503557, 1014.48014166, 1011.96203974,  997.27230198,
        997.87776226,  995.18792625, 1004.78744   , 1002.66537502,
        994.33141494, 1002.36896138, 1002.87835734,  995.98040641,
       1006.04119465, 1000.20961237,  995.8043948 ,  995.98781844,
        998.77570239,  998.30386426, 1006.25953686,  998.0188093 ,
        995.81853777,  997.72105433, 1006.61980185,  991.36115976])

Equação de Análise Empírica (Parte II)

Cálculo de

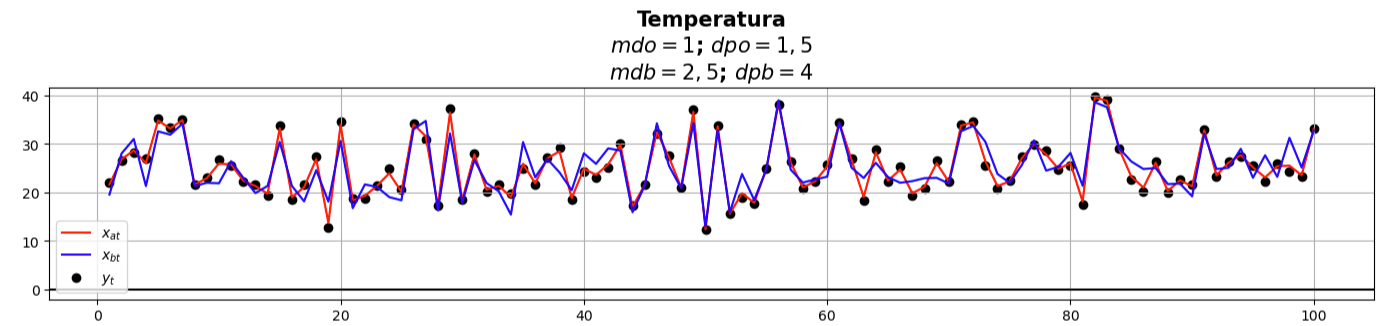
Equação de Análise Empírica (Parte II)

Cálculo de

Equação de Análise Empírica (Parte II)

Cálculo de

Equação de Análise Empírica (Parte II)

Conclusão

• Realizamos um ajustamento de curvas utilizando valores randômicos distribuídos normalmente para simular quantidades físicas
• Em ambos os casos, univariado e multivariado, conseguimos fazer com que o background se ajustasse às observações, de forma que parte do ruído do background foi filtrado
• Mesmo de forma bastante simples, estes dois exemplos mostram o que se pretende fazer com a assimilação de dados:
  • Utilizar o máximo de informações observacionais disponíveis para minimizar os efeitos do ruído no modelo (no sentido do método dos mínimos quadrados)
  • Corrigir e/ou atualizar o estado do background utilizando as observações

Notebook com Atividade Prática 2

Dúvidas

https://cfbastarz.github.io/met563-3/
https://github.com/cfbastarz/MET563-3
carlos.bastarz@inpe.br