Introdução à Assimilação de Dados (MET 563-3)

Motivação - Métodos Baseados em Conjuntos


Dr. Carlos Frederico Bastarz


Programa de Pós-Graduação em Meteorologia (PGMET) do INPE

05 de Outubro de 2025

🥷 🐦

Métodos Baseados em Conjuntos


Sumário


  1. Filtro de Kalman linear
  2. Método de Monte Carlo
  3. Ensembles
  4. Ensemble Kalman Filter
    4.1 Histórico e desenvolvimento
    4.2 Características principais
    4.3 Inflation
    4.4 Localização
  5. Visão geral sobre os esquemas derivados
  6. Atividades realizadas no CPTEC com o método LETKF
  7. Atividade - Filtro de Bayes Recursivo
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


1. Filtro de Kalman linear


  • O Filtro de Kalman calcula analiticamente a atualização do estado e da covariância, assumindo

    • Linearidade
    • Ruído gaussiano

  • Processo é realizado em duas etapas

    • Previsão
    • Correção

  • Na etapa de previsão

    • Ocorre a extrapolação do estado do modelo e da incerteza

  • Na etapa da correção

    • Ocorre o cálculo da matriz ganho de Kalman (matriz peso, tal como na Interpolação Ótima)
    • Ocorre a atualização da estimativa do estado com as observações
    • Ocorre a atualização da estimativa da incerteza
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


1. Filtro de Kalman linear


  • Etapa de previsão

    • 👉 Extrapolação do estado do modelo e da incerteza

    • Onde:
      • é o vetor background no tempo
      • é o modelo de previsão (linear), integrado do tempo até
      • é o vetor análise no tempo
      • é o erro do modelo, com covariância
      • é a covariância do background no tempo

  • Etapa da correção

    • 👉 Cálculo da matriz ganho de Kalman (matriz peso, tal como na Interpolação Ótima)

    • 👉 Atualização da estimativa do estado com as observações

    • 👉 Atualização da estimativa da incerteza

    • Onde:
      • é o vetor análise no tempo
      • é a covariância da análise no tempo
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


1. Filtro de Kalman linear


  • ✅ Vantagens do Filtro de Kalman linear
    • Além de estimar o estado do sistema (análise), estima analiticamente a covariância (incerteza)

      • Permite quantificar a confiança na análise

      • A matriz (ganho de Kalman) ajusta a contribuição do modelo e da observação


  • ❌ Limitações do Filtro de Kalman linear
    • Não é adequado para sistemas de alta dimensão (e.g., atmosfera, oceado), pois as matrizes de covariâncias ( e ) são explícitas e enormes
    • Requer que o modelo dinâmico seja linear
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


2. Método Monte Carlo


  • O método Monte Carlo foi introduzido nos anos 1940
    • John von Neumman, durante o desenvolvimento do projeto Manhattan (bomba atômica)

  • Premissa
    • 💡 Se não é possível calcular algo diretamente, pode-se estimar o resultado por meio de simulações aleatórias
    • Qualquer método estatístico baseado em amostragem massiva para obter resultados numéricos
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


2. Método Monte Carlo





  • 🎲 Exemplo simples
    • Estimar o valor de contando quantos pontos caem dentro de um quadrado que contém um círculo inscrito (a razão entre os pontos dentro do círculo e o total é )

Introdução à Assimilação de Dados (MET 563-3)

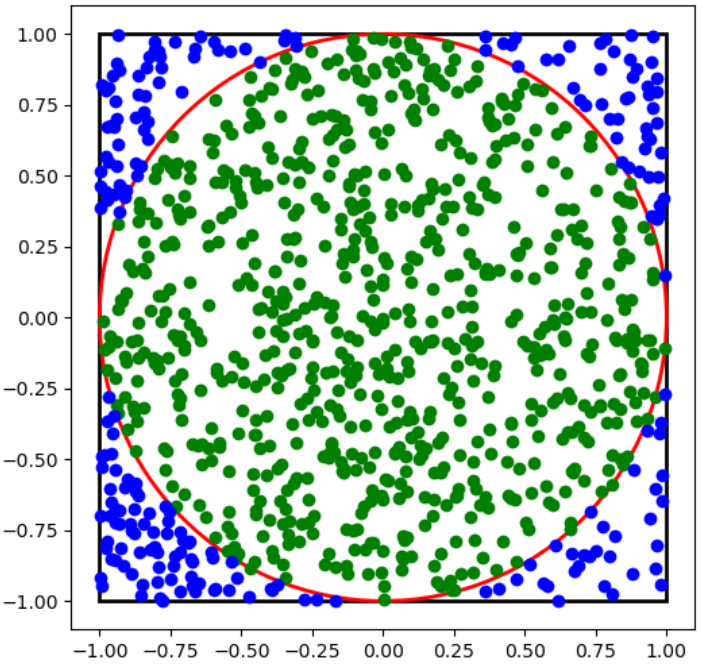
Métodos Baseados em Conjuntos


2. Método Monte Carlo


  • 🥧 Estimativa do valor de 

    import numpy as np

np.random.seed(42)

N = 1000000
x = np.random.rand(N)
y = np.random.rand(N)
dentro_circulo = (x**2 + y**2) <= 1

estima_pi = 4 * np.sum(dentro_circulo) / N
print(estima_pi)

  • 👉 Resultados

    Valores de N Valores de
    1 0,0
    10 2,8
    100 3,2
    1.000 3,112
    10.000 3,1556
    100.000 3,1376
    1.000.000 3,141864
    10.000.000 3,1415772
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


3. Ensembles

  • Ensemble ou conjunto (de análises ou previsões) representam múltiplas simulações para a mesma data alvo
    • O objetivo é tentar amostrar a incerteza do modelo
  • Diferentes técnicas podem ser utilizadas para se construir um ensemble
    • 👉 O mais simples: utilizar previsões de diferentes modelos (superensemble)
      • A desvantagem: pós-processar diferentes previsões de diferentes modelos
    • 👉 O mais complexo: utilizar assimilação de dados
      • A vantagem: fornece um ensemble de análises e previsões
    • Outras técnicas:
      • Poor man's ensemble: utiliza análises defasadas para gerar um ensemble inicial de previsões
      • Perturbação de física: utiliza diferentes parametrizações físicas do modelo para construir o ensemble
      • EOF: Funções Ortogonais Empíricas, utilizado pelo CPTEC
      • Singular Vectors: utilizado pelo ECMWF
      • Bred Vectors: utilizado pelo NCEP (passado)
      • EnKF: Ensemble Kalman Filter para assimilação de dados (e técnicas derivadas)
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos

3. Ensembles

  • Benefícios
    • Em geral, a média de um ensemble (bem construído) fornece uma boa estimativa em relação à previsão determinística (o skill tende a ser melhor)
    • Fornece também a incerteza da previsão (spread ou espalhamento do ensemble)

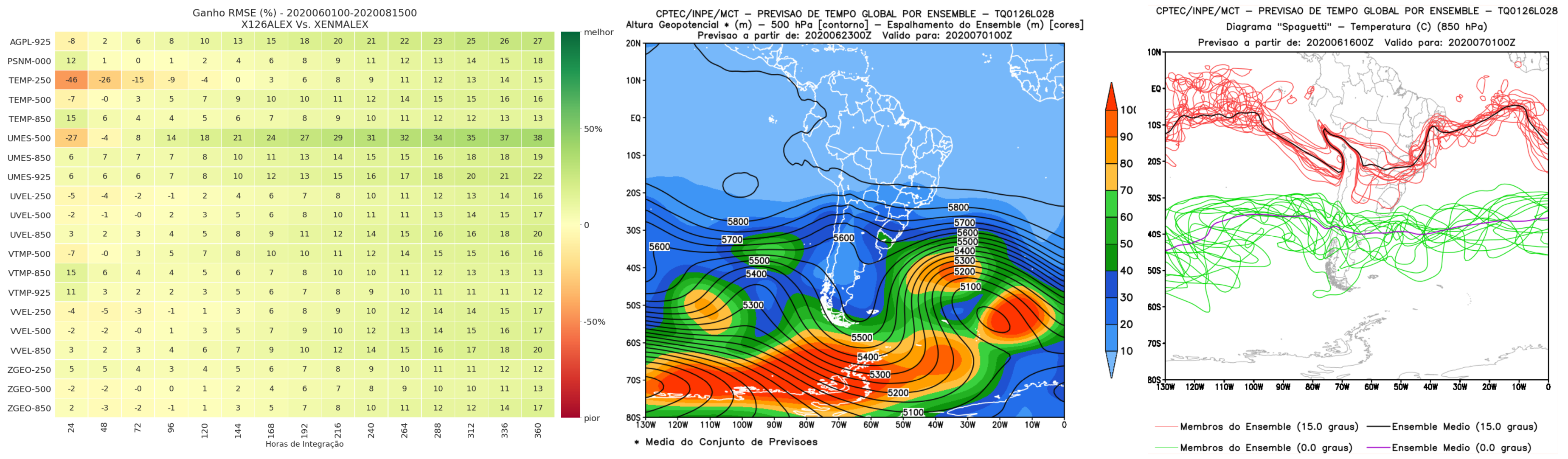
Métodos Baseados em Conjuntos

3. Ensembles

  • Desafios

    • Custo computacional (relação tamanho do ensemble X resolução espacial)

    • Armazenamento

    • Subestimativa da incerteza (undersampling) devido ao tamanho do ensemble

    • Acurácia e precisão



  • 🧠 Qual destas situações é acurada e precisa?
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos

3. Ensembles

  • As previsões de um modelo numérico podem conter viés e erros sistemáticos

    • O viés é uma medida do erro aleatório do modelo e está relacionado com a precisão na representação dos estados do modelo
      • 👉 Pode-se corrigir as previsões no pós-processamento
    • O erro sistemático está relacionado com a acurácia com a qual um modelo numérico representa estes estados
      • 👉 Deve-se corrigir o modelo antes que as previsões sejam feitas

Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


4. Ensemble Kalman Filter


4.1 Histórico e desenvolvimento


  • 📖 O Kalman Filter linear foi introduzido em 1960:
    • A New Approach to Linear Filtering and Prediction Problems (Kalman, 1960)
    • https://x.gd/VlIfX
  • 📖 O Ensemble Kalman Filter foi introduzido em 1994:
    • Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics (Evensen, 1994)
    • https://x.gd/VsQ1V
  • 💾 Com a evolução dos computadores e o aumento da complexidade do sistema de observação global, novas técnicas derivadas do EnKF surgiram:
    • EnSRF - Ensemble Square Root Filter
    • ETKF - Ensemble Transform Kalman Filter
    • LETKF - Local Ensemble Transform Kalman Filter
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


4. Ensemble Kalman Filter


4.2 Características principais


  • 👉 O Filtro de Kalman por conjunto é um filtro do tipo Monte Carlo
    • Assume que os erros são gaussianos
    • Assume que as relações entre os estados são lineares
    • Usa as matrizes de covariâncias para quantificar as incertezas

  • 💔 O problema

    • Em sistemas reais (e.g., atmosfera, oceano), é impossível armazenar e propagar a matriz de covariâncias completa

  • 💡 A solução

    • Ao invés de armazenar as matrizes de covariâncias (teóricas) gigantes, o EnKF estima estas matrizes a partir de um conjunto de amostras (ensemble)
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


4. Ensemble Kalman Filter


4.2 Características principais


  • O EnKF foi desenvolvido mantendo as principais características do filtro de Kalman linear, mas com as diferenças

    • 👉 Estimativa das covariâncias feita com base nos membros do ensemble e não via matriz explícitas

    • 👉 Matriz ganho de Kalman é conceitualmente igual, mas também calculada a partir do ensemble

    • 💡 A propagação das covariâncias é feita pela propagação do ensemble

    • 💡 Permite tratar a não linearidade, pois cada membro do ensemble pode evoluir pelo modelo não linear completo

    • O EnKF original é estocástico, no sentido de que as observações são perturbadas para gerar um conjunto de análises

Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


4. Ensemble Kalman Filter


4.2 Características principais


  • No EnKF, a covariância dos erros de previsão () é substituída pela covariância do conjunto

    • Onde:

      • é a matriz de perturbação do ensemble (desvio em relação à média)

    • 🧠 Por que é calculada considerando membros (fator de correção de Bessel)?

      • Usar no denominador do fator de correção, torna a estimativa tendenciosa, pois subestima a (co)variância real
      • Usar no denominador do fator de correção, evita a estimativa tendenciosa e coincide com a covariância verdadeira
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


4. Ensemble Kalman Filter


4.2 Características principais


  • Erro do modelo X Erro da previsão

  • Na equação da covariância do erro da previsão



  • Os termos e são semelhantes, mas possuem significados diferentes

    • representa a covariância total da incerteza do modelo (o quanto o EnKF confia nas previsões)
    • representa o erro introduzido pelo modelo (parametrizações, método numérico etc)
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


4. Ensemble Kalman Filter

4.2 Características principais

  • Se o conjunto for pequeno, as covariâncias são subestimadas
  • Quanto maior o conjunto, melhor será a representação das covariâncias
    • 🧠 Qual é o tamanho ideal de um conjunto para que se tenha a melhor estimativa das covariâncias do ("erro") do modelo?
  • Perturbação das observações

    • Cada observação é perturbada com um ruído aleatório, extraído da distribuição do erro de observação com covariância

    • Cada membro do ensemble recebe uma versão ligeiramente diferente das observações reais

    • O ruído é independente entre os membros e com média zero e covariância

    • 👉 Isso é o que garante que o EnKF não colapse, pois garante a dispersão (da covariância) do ensemble

Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


4. Ensemble Kalman Filter


4.3 Inflation


  • 🏃‍♂️‍➡️ No ciclo de assimilação de dados do EnKF, as observações são utilizadas para corrigir o estado do modelo
    • 💡 Mas o EnKF perturba o modelo para amostrar a sua incerteza
    • 🃏 Ambiguidade
      • Ao mesmo tempo que se perturba do estado, tenta-se corrigi-lo
    • 👉 Então, ao longo do tempo, a tendência é a de que a incerteza do EnKF seja cada vez mais subestimada, de forma que seja necessário inflar o spread (espalhamento ou incerteza) do conjunto
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


4. Ensemble Kalman Filter


4.3 Inflation


  • No EnKF, é estimada a partir de um número finito de membros

    • Como consequência, a estimativa da incerteza do modelo é subestimada

    • Isso faz com que o filtro confie mais nas previsões e menos nas observações!

    • Problemas podem ocorrer com a divergência do filtro

      • ⏳ Com o tempo, o modelo se afasta das observações

    • 💡 O inflation é um mecanismo artificial para aumentar a variância do ensemble





  • Cada membro é "inflado" em torno da média do ensemble 👉 é empírico!

  • Onde:

    • é o membro do ensemble com variância inflada
    • é a média do ensemble
    • é o fator de inflação ()

  • : não inflaciona o ensemble

  • : aumenta a dispersão do ensemble 👉 aumenta a incerteza 👉 aumenta a variância

  • : diminui a dispersão do ensemble 👉 diminui a incerteza 👉 diminui a variância

  • Se o ensemble for pequeno, maior é o valor de

Métodos Baseados em Conjuntos


4. Ensemble Kalman Filter


4.3 Inflation


  • A escolha de um valor para é empírica e depende do tamanho do ensemble
    • Quanto menor o ensemble, maior pode ser o valor de
  • O inflation pode ser implementado de forma que seja adaptativo
    • Pode variar em função do spread e do erro da análise

Métodos Baseados em Conjuntos


4. Ensemble Kalman Filter

4.3 Localização

  • A localização é utilizada para compensar o efeito cíclico de correções sobre o espalhamento do conjunto de previsões devido ao seu tamanho, para evitar
    • Covariâncias espúrias
      • Se o ensemble for pequeno, a amostragem das covariâncias é ruim, o que faz com que covariâncias distantes não reflitam as relações físicas reais
    • Custo computacional alto

      • A localização limita a covariância entre variáveis de estado que estão muito longe umas das outras

      • Onde:

        • é uma função de correlação (funciona como um raio de influência)
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


5. Visão geral sobre os esquemas derivados


  • EKF - Extended Kalman Filter

    • É uma extensão do Filtro de Kalman linear para sistemas não lineares
    • Lineariza o modelo e o operador observação ao redor do estado estimado

  • EnSRF - Ensemble Square Root Filter

    • É a forma determinística do EnKF (o EnKF é estocástico porque perturba as observações!)
    • Cada membro é atualizado em torno da média do ensemble

  • LETKF - Local Ensemble Kalman Filter

    • Atualiza cada ponto de grade de forma independente no espaço do ensemble (é mais eficiente)
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


5. Visão geral sobre os esquemas derivados


EKF - Extended Kalman Filter


  • É uma extensão do Filtro de Kalman linear para sistemas não lineares (não é ensemble!)
  • Lineariza o modelo e o operador observação ao redor do estado estimado

  • Equações do modelo

  • Equações da análise


  • Onde:
    • é a matriz jacobiana do operador observação
    • é a matriz jacobiana do operador observação
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


5. Visão geral sobre os esquemas derivados


EnSRF - Ensemble Square Root Filter


  • É a forma determinística do EnKF (o EnKF é estocástico porque perturba as observações!)
  • Cada membro é atualizado em torno da média do ensemble

  • Atualização do ensemble médio (análise)

  • Atualização das anomalias (covariâncias)

  • Onde:

    • e são covariâncias cruzadas entre o espaço do modelo e o espaço físico (observações)
    • é a matriz square root (raiz quadrada) que garante que as covariâncias do ensemble correspondam às covariâncias do filtro de Kalman linear, sem precisar perturbar as observações
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


5. Visão geral sobre os esquemas derivados


LETKF - Local Ensemble Kalman Filter


  • Atualiza cada ponto de grade de forma independente no espaço do ensemble (é mais eficiente)

  • Matriz peso da análise () no espaço do ensemble:


  • Matriz de ganho transformado

  • Atualização da média e anomalias no espaço dos pesos

  • Equação da análise no espaço do modelo

  • Onde:
    • são os vetores unitários que definem cada membro no espaço reduzido do ensemble
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


6. Atividades realizadas no CPTEC com o método LETKF


  • Por volta de 2009, o grupo de assimilação de dados do CPTEC vinha estudando a aplicação do LETKF como método substituto para a sua análise operacional em domínio global
    • Resolução: TQ0126L028 (aproximadamente 100 km de resolução espacial horizontal e 28 níveis verticais em coordenada sigma)
    • 40 membros

  • 🔨 Desafios
    • Desempenho computacional para um conjunto grande de membros (aumento da resolução ficou limitado ao tamanho do conjunto)
    • Assimilação de radiâncias (necessidade de desenvolvimento de diferentes operadores para diferentes tipos de observações não convencionais)
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


6. Atividades realizadas no CPTEC com o método LETKF


  • LETKF permaneceu como método de pesquisa do CPTEC
    • 2010 - Tese Rosângela Cintra: "Assimilação de Dados com Redes Neurais Artificiais em Modelo de Circulação Geral da Atmosfera"
    • 2010 - Pós-Doutorado José Aravéquia: "Evaluation of a Strategy for the Assimilation of Satellite Radiance Observations with the Local Ensemble Transform Kalman Filter"
    • 2011 - Dissertação Maria Medeiros: "Impacto do Uso de Radiância na Assimilação de Dados usando 4D-LETKF na Região da América do Sul"
    • 2013 - Bolsa PCI Lucas Avanço: "Assimilação de Dados de Rádio Ocultação GNSS no LETKF: Disponibilidade de Dados e Implementação de um Operador"
    • 2018 - Tese Helena Barbieri: "Ajuste Dinâmico para Análise Híbrida entre um Sistema Variacional e Filtro de Kalman por Conjunto"
    • 2018 - Tese Leonardo Lima: "Estudo das Incertezas na Simulação por Conjuntos e no Uso da Assimilação de Dados no Oceano Atlântico Sudoeste"
    • Entre outros...
Introdução à Assimilação de Dados (MET 563-3)


Ninja Vs. Codorna

🥷 🐦

Métodos Baseados em Conjuntos


7. Atividade - Filtro de Bayes Recursivo






Ninja Vs. Codorna

🥷 🐦



  • Uma codorna 🐦 pia no meio da mata
  • Um ninja 🥷 escuta...
  • A codorna pia mais uma vez
  • O ninja escuta novamente...
  • O ninja quer saber onde está a codorna
  • A codorna pia novamente...
  • E ela faz isso mais 100 vezes
  • Pergunta
    • 🧠 Será o ninja capaz de descobrir a posição da codorna no meio da mata? (continua...)

Métodos Baseados em Conjuntos


7. Atividade - Filtro de Bayes Recursivo


  • Palavras-chave

    • Hipótese: uma pergunta - uma teoria seria uma afirmação?
    • Dado: uma informação, uma observação
    • Verossimilhança: (ou likelihood) o grau de veracidade de uma determinada informação
    • Informação à priori: (ou prior) aquilo que se conhece a princípio
    • Informação à posteriori: (ou posterior) aquilo que se conclui a partir da informação à priori
    • Probabilidade conjunta: probabilidade de dois ou mais eventos ocorrerem simultaneamente

  • Conceito-chave

    • Probabilidade condicional: ocorrência de um evento dada uma informação à priori
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


7. Atividade - Filtro de Bayes Recursivo


  • Teorema de Bayes

  • Onde:
    • : é a hipótese
    • : é o dado observado (uma informação observada)
    • : é o posterior (ou posteriori, é a probabilidade da hipotese após observar o dado)
    • : é o prior (é a probabilidade atribuída à hipótese antes de ver o dado)
    • : é a probabilidade do dado (constante de normalização)
    • : verossimilhança (é a probabilidade da observar o dado, considerando-se a hipótese verdadeira)
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


7. Atividade - Filtro de Bayes Recursivo


Probabilidade Vs. Verossimilhança


  • Probabilidade
    • É a chance de ocorrência de um determinado evento possível
  • Verossimilhança
    • É provável (ou possível) que este evento exista? Este evento é plausível?

  • Para que um determinado evento ocorra, é necessário que ele exista e que pertença a um determinado conjunto de eventos possíveis
    • A máxima verossimilhança destaca, portanto, o quão verossímil é a probabilidade do evento
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


7. Atividade - Filtro de Bayes Recursivo


Verossimilhança


  • Considere que você observa o lançamento de 20 dados 🎲 sobre uma mesa e deseja saber qual é a verossimilhança desta observação - todos os dados apresentam os mesmos valores

  • Para isto, consideramos duas hipóteses:
    1. Dado viciado
    2. Dado não viciado
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


7. Atividade - Filtro de Bayes Recursivo


🎲 Dado viciado

  • Neste cado, os 20 dados apresentam o mesmo valor (e.g., 5)

    • A probabilidade conjunta destes eventos

🎲 Dado não viciado

  • Neste caso, cada um dos 20 dados possui a mesma probabilidade de apresentar um dos 6 números possíveis

    • A probabilidade conjunta neste caso é

  • 👉 Portanto, é muito mais verossímil que o dado seja viciado dada a observação inicial

Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


7. Atividade - Filtro de Bayes Recursivo


Provabilidade Vs. Verossimilhança

  • Exemplo

    • : o ninja 🥷 ouve um canto na mata

    • : há uma codorna 🐦 na mata

    • : é a verossimilhança

      • : o fato de o ninja ouvir um canto na mata, dado que há uma codorna na mata, não significa que dado que há uma codorna na mata, o ninja ouvirá um canto - ela pode estar dormindo 🐦 💤
      • , então é baixa: se há uma codorna na mata, não necessariamente ela está cantando e o que o ninja ouve não é uma codorna, mas sim um pardal 🐦
      • , então é alta: se há uma codorna na mata, então há um canto ecoando na mata
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


7. Atividade - Filtro de Bayes Recursivo


Estimativa de Máxima Verossimilhança


  • Permite estimar, por exemplo, os momentos estatísticos de uma determinada distribuição. Por exemplo:
    • Quais são os valores de média () e desvio-padrão () que maximizam a probabilidade de um determinado evento (ou hipótese) ou dado observado?
    • Em outras palavras, quais são os valores de e que tornam os dados observados mais prováveis (considerando que os dados vem de uma distribuição normal )?
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


7. Atividade - Filtro de Bayes Recursivo


Exemplo de Inferência Bayesiana (ou Filtro Bayesiano)


  • Kalnay (2002)🔸: dadas duas observações independentes e , as quais são assumidas possuírem distribuição normal e erros com desvios-padrão e , qual é o valor mais provável de ? Neste caso, define-se a análise como sendo o valor mais provável de dadas as observações e as suas estatísticas de erro:

🔸Kalnay, E. (2002). Atmospheric Modeling, Data Assimilation and Predictability. Cambridge: Cambridge University Press.

Métodos Baseados em Conjuntos


7. Atividade - Filtro de Bayes Recursivo

  • Distribuição Normal - ou Gaussiana

  • O valor mais provável (likely) de dadas as observações independentes e , é aquele que maximiza a probabilidade conjunta, ou seja, o produto de e :

Métodos Baseados em Conjuntos


7. Atividade - Filtro de Bayes Recursivo


Prior, posterior, likelihood, distribuição de probabilidade...


  • Teorema de Bayes

  • Distribuição Gaussiana

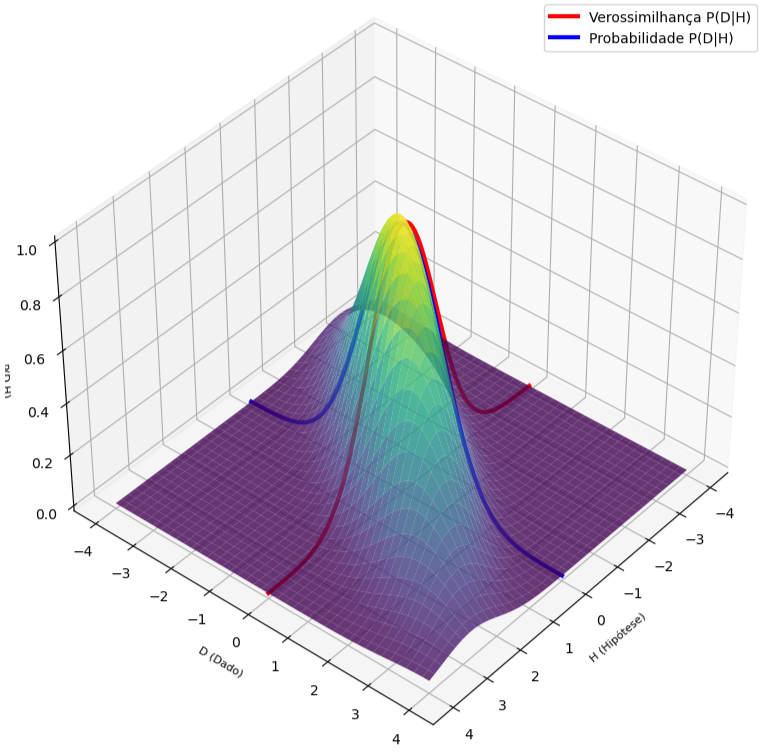
Métodos Baseados em Conjuntos


7. Atividade - Filtro de Bayes Recursivo


Inferência Bayesiana Recursiva (ou "Filtro de Bayes Recursivo")


  • Um ninja ouve o canto intermitente de uma codorna (ela está parada)
  • A cada canto, ele tenta descobrir a posição da codorna
    • 🧠 Como o ninja pode inferir a posição da codorna?

  • Um outro problema real poderia ser: ajustar um modelo aos valores observados a cada ciclo de análise
    • 🧠 Como isso pode ser feito de forma iterativa?
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


7. Atividade - Filtro de Bayes Recursivo


Exemplo prático: Ninja Vs. Codorna

  • Método Monte Carlo
    • 🔴 posição real da codorna
    • ➕ posição da codorna, segundo o ninja ()
  • A cada canto da codorna, o ninja tenta descobrir a posição real da ave
  • O ninja pode modelar a situação e, com um número finito de tentativas, pode estimar a posição mais provável da codorna
Introdução à Assimilação de Dados (MET 563-3)

Métodos Baseados em Conjuntos


7. Atividade - Filtro de Bayes Recursivo






  • Para cada posição inferida pelo ninja, a "função iterativa de Bayes", calcula a verossimilhança da posição:
m[i,j] =  norm * np.exp(np.matmul(-(x[:,n] - me), np.matmul(inv, (x[:,n] - me) / 2.)))
  • Ou seja,

  • A melhor estimativa obtida pelo ninja utilizando-se a inferência Bayesiana recursiva, é chamada de "Estimativa de Máxima Verossimilhança" e representa o valor mais provável a ser obtido (cores mais quentes na superfície) da posição da codorna

Métodos Baseados em Conjuntos


7. Atividade - Filtro de Bayes Recursivo


🎲 Notebook com Atividade Prática 7

Introdução à Assimilação de Dados (MET 563-3)

🤔 Dúvidas








🔗 https://cfbastarz.github.io/met563-3/
🐙 https://github.com/cfbastarz/MET563-3
📧 carlos.bastarz@inpe.br






👉 This work is licensed under CC BY-NC-SA 4.0

Introdução à Assimilação de Dados (MET 563-3)

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style

Scoped style