Histórico da Assimilação de Dados

Marcos Históricos no Mundo

• Richardson, 1922: Weather Prediction by Numerical Process (https://x.gd/4ccVg)
  • Primeira tentativa de análise objetiva manual
• Panofsky, 1949: Objective Weather Map Analysis (https://x.gd/sBmUk)
  • Ajuste do campo de análise por meio de um polinômio interpolador global
• Bergthórsson e Döös, 1955: Numerical Weather Map Analysis (https://x.gd/qmxVS)
  • Combinação de background e observações
• Cressman, 1959: An Operational Objective Analysis System (https://x.gd/DkMuD)
  • Acrescenta raio de influência
• Gandin, 1963: Objective Analysis of Meteorological Fields (https://x.gd/TKtbo)
  • Formalização estatística
• BLUE^🔸 e métodos modernos
  • Modelagem explícita das estatísticas

Histórico da Assimilação de Dados

Análise Subjetiva

• Análise produzida manualmente pelo meteorologista previsor (analista) a partir de observações distribuídas irregularmente
  • Depende muito da experiência e conhecimento físico do analista sobre a atmosfera
  • Muito utilizada até a década de 1950, antes do uso dos computadores digitais para a previsão numérica de tempo
  • Resultados difíceis de reproduzir devido à subjetividade do analista

Histórico da Assimilação de Dados

Análise Objetiva

• Análise produzida por meio de algorítmos matemáticos e estatísticos para transformar dados observacionais irregulares em campos regulares (grades)
  • Utiliza métodos estatísticos, interpolação, ponderação por erro e covariância
  • Resultados podem ser reproduzíveis
  • Permite a automatização dos processos e uso em larga escala
  • Reduz a subjetividade
  • Necessidade da modelagem dos erros e correlações espaciais

Histórico da Assimilação de Dados

Lewis Fry Richardson

• Pioneiro da Previsão Numérica do Tempo:
  • Propôs usar equações da dinâmica resolvidas numericamente para prever o tempo
  • Resolveu manualmente uma previsão de 6 horas para a pressão atmosférica (levou semanas); o resultado foi ruim, mas revolucionário
• Fábricas de previsões:
  • Imaginou centros com centenas de pessoas calculando em paralelo diferentes regiões do planeta
• Equações numéricas:
  • Propôs métodos iniciais de discretização das equações atmosféricas (diferenças finitas), uma das sementes do desenvolvimento posterior de modelos como ENIACC

Histórico da Assimilação de Dados

O mundo nos anos 1950

• Pós segunda guerra mundial
• Início da guerra fria
• Primeiros computadores comerciais (UNIVAC - 1951)
  • Transistores já começaram a substituir as válvulas
• Motores a jato chegam à aviação comercial
• Corrida espacial (URSS lança o Sputnik 1 - 1957)
• Criação da NASA - 1958
• Testes com mísseis balísticos

Histórico da Assimilação de Dados

Tecnologia nos anos 1950

• Na imagem ao lado, máquina IBM^🔸 704 (1954) na NACA^🔸
  • Fonte: https://en.wikipedia.org/wiki/IBM_704

Histórico da Assimilação de Dados

Tecnologia nos anos 1950

• Na imagem ao lado, exemplo de máquina teletipo utilizada pela NOAA^🔸
  • Fonte: https://www.galleyrack.com/images/artifice/telegraphy/tty/gallery/noaa/wea01816.jpg

Histórico da Assimilação de Dados

Tecnologia nos anos 1950

• Na imagem ao lado, exemplo de mapa de teclado de uma máquina teletipo para uso em previsão de tempo
  • Fonte: https://upload.wikimedia.org/wikipedia/commons/a/a7/WeatherTeletypeChart.jpg

Histórico da Assimilação de Dados

Tecnologia nos anos 1950

• Na imagem ao lado, exemplo de uma carta sinótica impressa por uma máquina teletipo
  • Fonte: https://www.galleyrack.com/images/artifice/telegraphy/tty/gallery/noaa/wea01819.jpg

Histórico da Assimilação de Dados

Até 1954

• Primeiros experimentos em PNT foram realizados por meio da análise subjetiva (interpolação manual das observações em ponto de grade)
• Primeiras tentativas de análise objetiva (interpolação matemática das observações):
  • Panofsky, 1949: polonômio "global" (o mesmo polinômio é usado em toda a grade)
    • Problema: como tratar regiões com poucas observações?
  • Gilchrist e Cressman (1954): polinômio "local" (um polinômio é definido para cada ponto de grade)

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

Características Principais

• Novo método para a análise (objetiva) meteorológical espacial
• Automatiza o processo de análise objetiva de forma rápida e eficiente (se comparada com análise subjetiva convencional)
• Precursor do método de correções sucessivas
• Necessidade de um background ou climatologia ou uma combinação de ambos

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

Características Principais

• Pesos empíricos são atribuídos ao background e observações (função da distância entre o ponto de grade e ponto da observação)
• Erros não correlacionados entre background e observações
• Erro do background é homogêneo (igual em todos os pontos de grade) e a variância é independente do local
• O erro da observação é espacialmente não correlacionado (cada estação tem o seu erro) e é uma função apenas do erro do instrumento

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

Detalhes da formulação (seguindo Daley, 1991^🔸)

• Considere uma única observação no ponto
• Considere duas estimativas de no ponto de grade :

• Onde,
  • é o background no ponto de grade
  • é a diferença entre a observação e o background , sendo esta diferença constante ao longo da curva que une os pontos de grade e

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

Detalhes da formulação (seguindo Daley, 1991^🔸)

• A análise de Bergthórsson e Döös combina estas duas estimativas da seguinte forma:

• O que acontece quanto às posições relativas do ponto de estação e do ponto de grade:
  • Quando (pontos de grade e estação coincidem), então
  • Quando (distância entre os pontos aumenta), então

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

Exemplo 1D

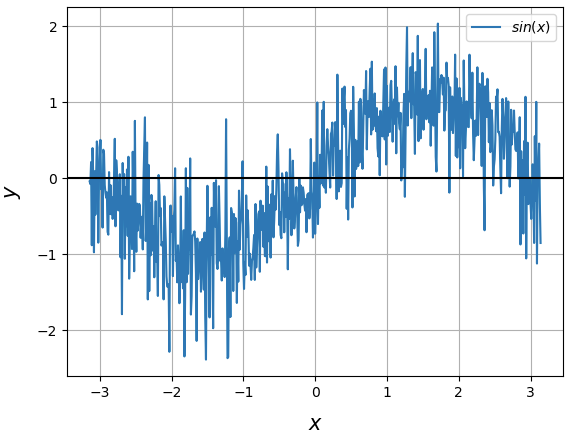
• Considere um modelo matemático simples:

• A função seno com a adição de um ruído normalmente distribuído

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

Exemplo 1D

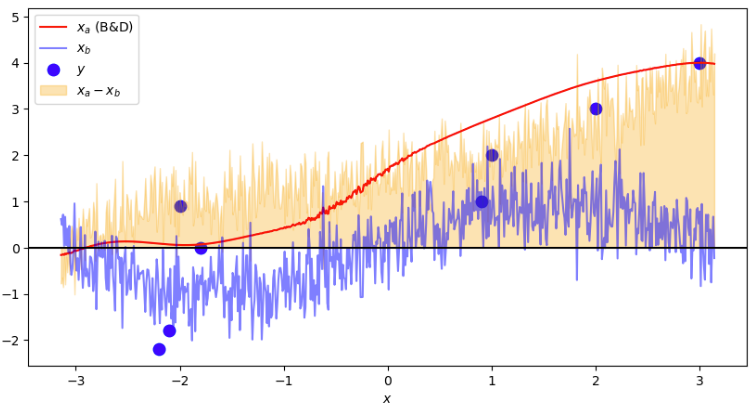
• Dentro do domínio do nosso modelo, definimos algumas observações, junto com as suas posições (ambos arbitrários):

# Posições

obs_pos = np.array([-2.2, -2.1, -2.0, -1.8, 0.9, 1, 2, 3])

# Valores medidos

obs_vals = np.array([-2.2, -1.8, 0.9, 0, 1, 2, 3, 4])  

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

Exemplo 1D

• Definiremos uma função peso Gaussiana simplificada que terá o mesmo efeito proposto por Bergthórsson e Döös (1955)
• é o desvio-padrão e sua função é a de modular a influência das observações na análise

def weight(dx, L=L):
    return np.exp(-(dx**2)/(2*L**2))

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

Exemplo 1D

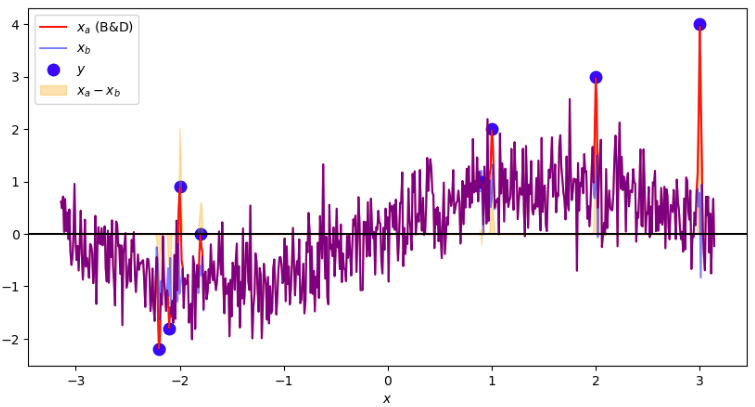
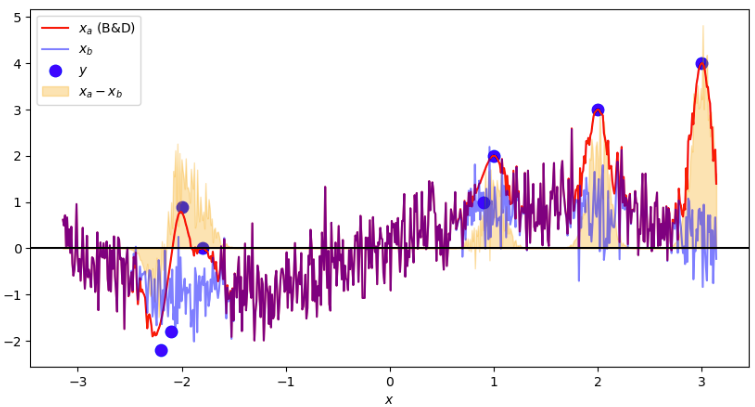
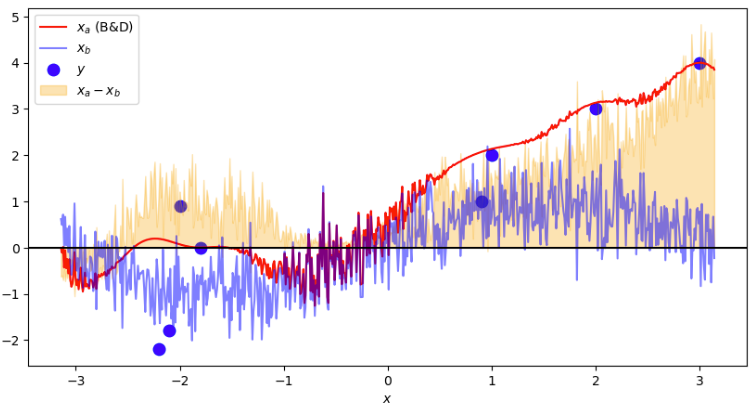
• Inicializamos a análise como sendo o background
• Aplicamos a função para cada observação contida dentro do domínio
• A depender o valor de , a análise resultante será mais ou menos influenciada pelas observações

# Inicializa análise como background

xa = xb.copy()


# Aplica a correção observação por observação

for xo, yo in zip(obs_pos, obs_vals):
    dx = x - xo
    w = weight(dx, L=L)
    xa = (1-w)*xa + w*yo

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

Exemplo 1D

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

Exemplo 1D

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

Exemplo 1D

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

Exemplo 1D

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

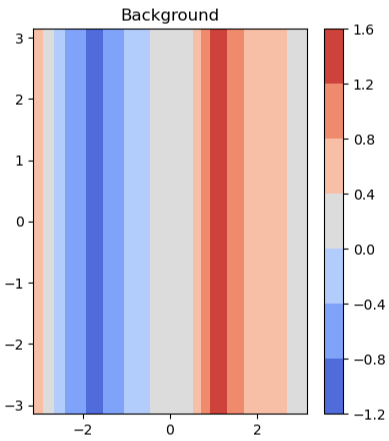
Exemplo 2D

• Considere um modelo matemático simples:

• A função seno com a adição de um ruído normalmente distribuído
• Definimos um plano Cartesiano de 100 pontos onde esta função será aplicada

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

Exemplo 2D

• Iniciamos com a definição do domínio e da malha onde o modelo será aplicado:

lon = np.linspace(-np.pi, np.pi, 10)
lat = np.linspace(-np.pi, np.pi, 10)

LON, LAT = np.meshgrid(lon, lat)

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

Exemplo 2D

• Resolvemos o modelo para todos os pontos do domínio, somando o ruído normalmente distribuído ao final:

xb_seno = np.sin(LON)

sigma = 0.5  # desvio-padrão do ruído
ruido = np.random.randn(len(LON)) * sigma 

xb = xb_seno + ruido

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

Exemplo 2D

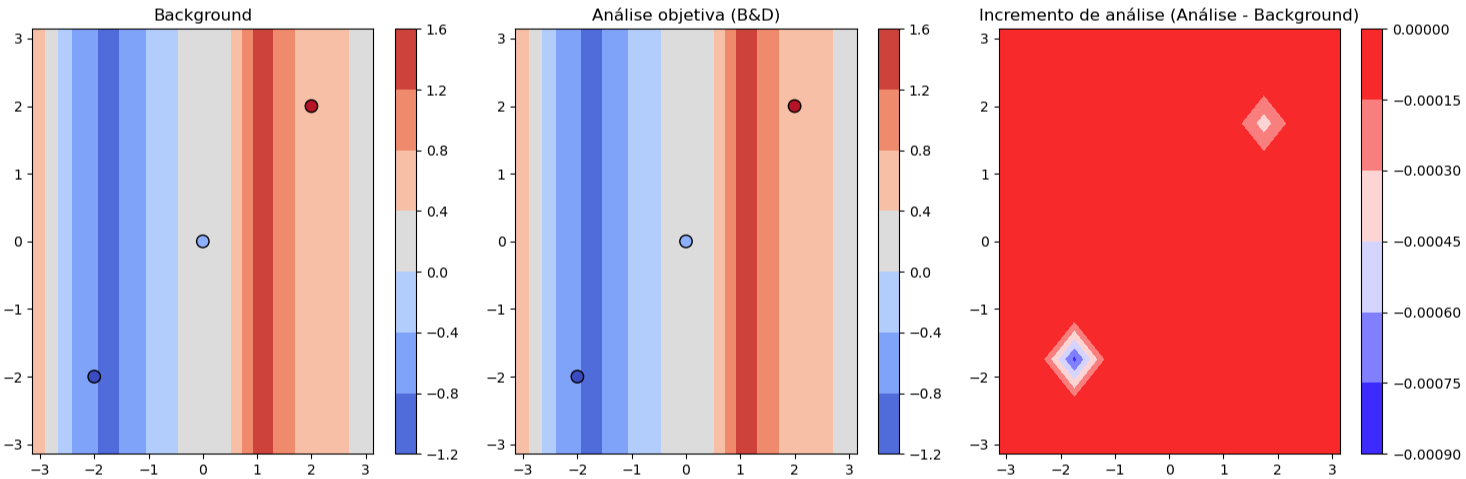
• Em seguida, determinamos junto com a sua posição, algumas observações a serem consideradas dentro do domínio:

# Posições

obs_locs = np.array([[-2, -2],
                    [0, 0],
                    [2, 2]])

# Valores medidos

obs_vals = np.array([-1.5, -1.0, 0.5])

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

Exemplo 2D

• Definiremos uma função peso Gaussiana simplificada que terá o mesmo efeito proposto por Bergthórsson e Döös (1955)
• é o desvio-padrão e sua função é a de modular a influência das observações na análise

def weight(dx, dy, L=L):    
    return np.exp(-(dx**2 + dy**2)/(2*L**2))

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

Exemplo 2D

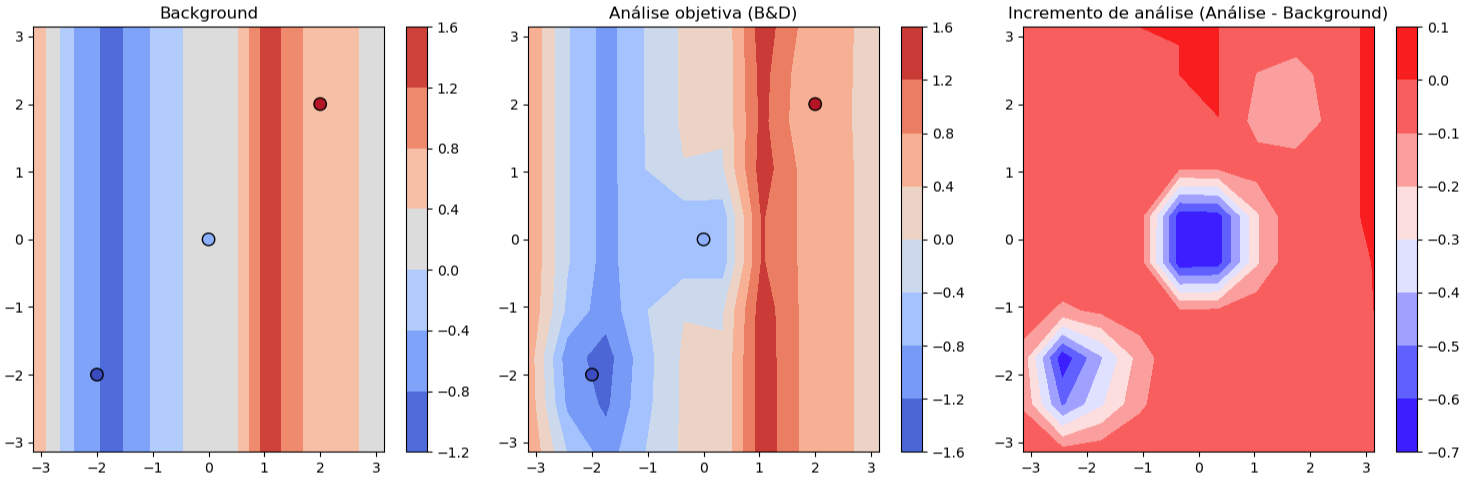
• Inicializamos a análise com sendo o background
• Aplicamos a função para cada observação contida dentro do domínio
• A depender do valor de , a análise resultante será mais ou menos influenciada pelas observações

# Inicializa a análise como background

xa = xb.copy()


# Aplica a correção observação por observação

for (xo, yo), obs in zip(obs_locs, obs_vals):
    dx = LON - xo
    dy = LAT - yo
    w = weight(dx, dy, L=L) 
    xa = (1-w) * xa + w * obs

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

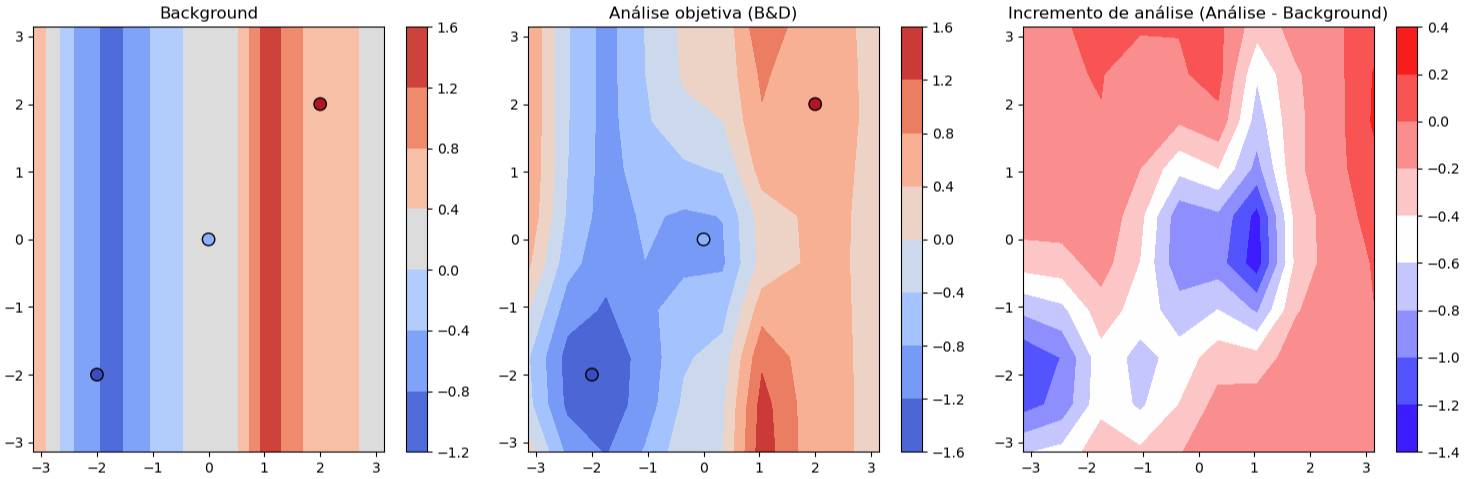
Exemplo 2D

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

Exemplo 2D

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

Exemplo 2D

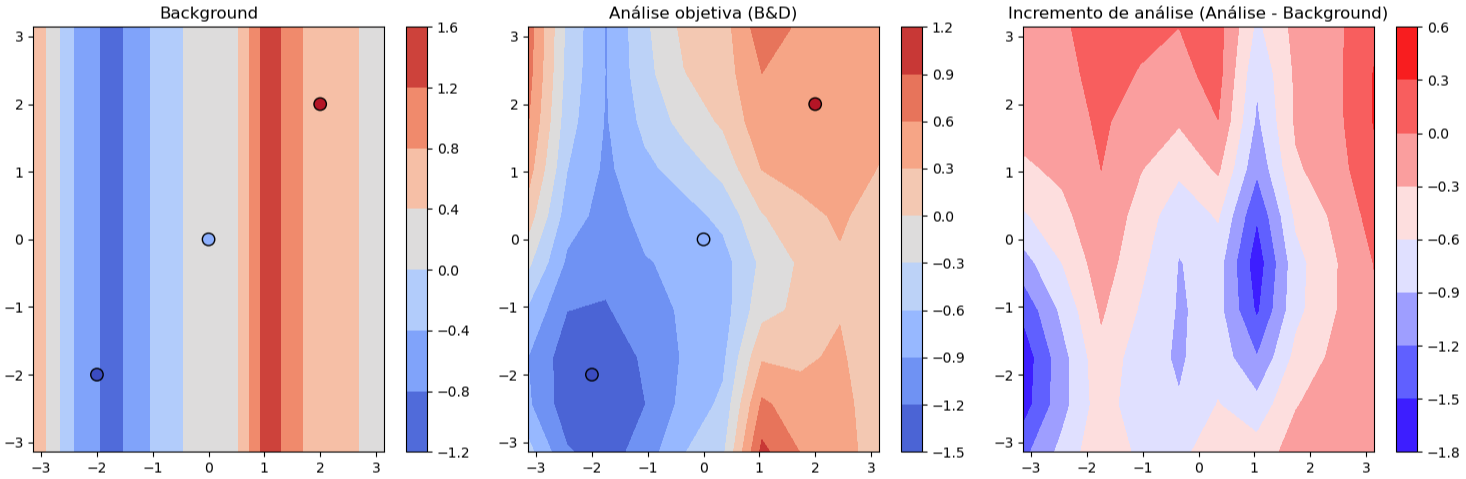
Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

Exemplo 2D

Histórico da Assimilação de Dados

Numerical Weather Map Analysis (Bergthórsson e Döös, 1955)

Notebook com Atividade Prática 3

Dúvidas

https://cfbastarz.github.io/met563-3/
https://github.com/cfbastarz/MET563-3
carlos.bastarz@inpe.br